
一個分布要么是對稱的,當高的值和低的值相互平衡抵消;要么有偏斜,當非對稱并且在高值和低值間不平衡。要判定一組數(shù)據(jù)的形狀,我們必須比較均值和中位數(shù)。如果這兩個值相等,CTQ或者X被認為對稱的(零偏斜)。如果均值小于中位數(shù),變量被稱為負偏斜,又叫左偏斜。如果均值大于中位數(shù),變量被稱為正偏斜,又叫右偏斜。因此:
均值>中位數(shù):正偏斜(positive),又叫右偏斜。
均值<中位數(shù):負偏斜(negative),又叫左偏斜。
均值=中位數(shù):對稱的(symmetry),又叫零偏斜。
當均值由于某些非正常的大數(shù)值而增加時,正偏斜會發(fā)生。當均值由于某些非正常的小數(shù)值而減少時,負偏斜會發(fā)生。當分布為對稱形狀時,是沒有某一極端方向特別的數(shù)據(jù)出現(xiàn)的(見圖1)。

圖1 三組數(shù)據(jù)的分布形狀比較
圖1a中的數(shù)據(jù)是負偏斜的,又叫左偏斜。在此圖中,有一個由于某些特別小的數(shù)據(jù)引起的長尾和偏向左側(cè)的彎曲。這些特別小的數(shù)據(jù)將會使均值減小以致均值小于中位數(shù)。圖1b中是對稱的,曲線兩側(cè)部分和對方對稱,大小值相互平衡,均值等于中位數(shù)。圖1c為正偏斜,又叫右偏斜。在此圖中有一個由于某些特別大的數(shù)據(jù)引起的長尾和偏向右側(cè)的彎曲。這些特別大的數(shù)據(jù)將會使均值變大以致均值大于中位數(shù)。
在下表中,Minitab計算偏斜統(tǒng)計量等于0.10,因為此數(shù)很接近于零,我們可以得出如下結(jié)論:訂單完成時間是對稱的。

使用Minitab計算完成時間的描述性統(tǒng)計
為了判定一組數(shù)據(jù)是對稱的或者有偏斜的,我們可以考慮在樣本值分布中是否有超過一個的集中值(concentrations)。有兩個集中值的分布被稱為雙峰的(bimodal)。雙峰分布的存在常常意味著這組數(shù)據(jù)是由兩組數(shù)據(jù)被不合理的結(jié)合在一起的。
為了說明雙峰分布,有一家銀行收集了200個在高峰期抵達的客戶的樣本數(shù)據(jù)來判定客戶的原意等待時間。圖2為用Minitab直方圖表示的等待時間:
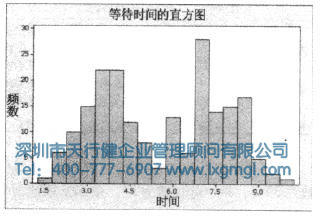
圖2 等待時間的Minitab直方圖
在等待時間的分布上有兩個波峰,一個在3.5和4.5之間,另外一個在6和7.5之間。事實上,這些數(shù)據(jù)是來自一家銀行的兩個不同分行的。第一家分行的等待時間數(shù)據(jù)是來源于周五中午12點到下午2點(這家分行位于城市的中心商業(yè)區(qū))。第二家分行的等待時間數(shù)據(jù)是來源于周五下午5點到下午7點(這家分行位于居民區(qū))。
圖3為兩家分行等待時間的Minitab點圖:
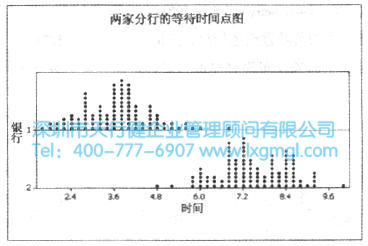
圖3 顧客等待時間的Minitab點圖
從圖3我們可以發(fā)現(xiàn)兩家分行的顧客等待時間分布是不同的。第一家分行的顧客等待時間分布集中于3~4分鐘,而第二家分行的顧客等待時間集中在7~8分鐘。